Linear Algebra
- mathematics of data: multivariate, least square, variance, covariance, PCA
- equotion: y =
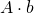 , where A is a matrix, b is a vector of depency variable
, where A is a matrix, b is a vector of depency variable - application in ML
- Dataset and Data Files
- Images and Photographs
- One Hot Encoding: A one hot encoding is a representation of categorical variables as binary vectors.
encoded = to_categorical(data) - Linear Regression. L1 and L2
- Regularization
- Principal Component Analysis. PCA
- Singular-Value Decomposition. SVD. M=U*S*V
- Latent Semantic Analysis. LSA typically, we use
tf-idfrather than number of terms. Through SVD, we know the different docments with same topic or the different terms with same topic - Recommender Systems.
- Deep Learning
Numpy
- array broadcasting
- add a scalar or one dimension matrix to another matrix.
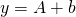 where b is broadcated.
where b is broadcated. - it oly works when when the shape of each dimension in the arrays are equal or one has the dimension size of 1.
- The dimensions are considered in reverse order, starting with the trailing dimension;
- add a scalar or one dimension matrix to another matrix.
Matrice
- Vector
- lower letter.
- Addtion, Substruction
- Multiplication, Divsion(Same length) a*b or
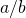
- Dot product:
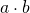
- lower letter.
- Vector Norm
- Defination: the length of vector
- L1. Manhattan Norm.
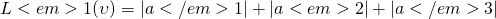
python: norm(vector, 1). Keep coeffiencents of model samll - L2. Euclidean Norm.
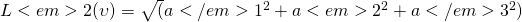
python: norm(vector) - Max Norm.
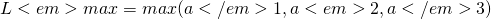
python: norm(vector, inf)
- Matrices
- upper letter.
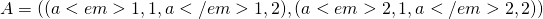
- Addtion, substruction(same dimension)
- Multiplication, Divsion( same dimension)
- Matrix dot product. If
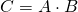 , A’s column(n) need to be same size to B’s row(m).
, A’s column(n) need to be same size to B’s row(m). python: A.dot(B) or A@B - Matrix-Vector dot product.
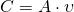
- Matrix-Scalar. element-wise multiplication
- Type of Matrix
- square matrix. m=n. readily to add, mulitpy, rotate
- symmetric matrix.
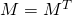
- triangular matrix.
python: tril(vector) or triu(vector)lower tri or upper tri matrix - Diagonal matrix. only diagonal line has value, doesnot have to be square matrix.
python: diag(vector) - identity matrix. Do not change vector when multiply to it. notatoin as
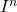
python: identity(dimension) - orthogonal matrix. Two vectors are orthogonal when dot product is zeor.
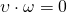 or
or 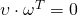 . which means the project of
. which means the project of 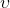 to
to 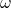 is zero. An orthogonal matrix is a matrix which
is zero. An orthogonal matrix is a matrix which 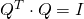
- Matrix Operation
- Transpose.
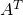 number of rows and columns filpped.
number of rows and columns filpped. python: A.T - Inverse.
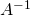 where
where 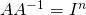
python: inv(A) - Trace.
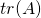 the sum of the values on the main diagonal of matrix.
the sum of the values on the main diagonal of matrix. python: trace(A) - Determinant. a square matrix is a scalar representation of the volume of the matrix. It tell the matrix is invertable.
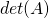 or
or  .
. python: det(A). - Rank. Number of linear indepent row or column(which is less). The number of dimesions spanned by all vectors in the matrix.
python: rank(A)
- Transpose.
- Sparse matrix
- sparsity score =
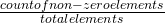
- example: word2vector
- space and time complexity
- Data and preperation
- record count of activity: match movie, listen a song, buy a product. It usually be encoded as : one hot, count encoding, TF-IDF
- Area: NLP, Recomand system, Computer vision with lots of black pixel.
- Solution to represent sparse matrix. reference
- Dictionary of keys: (row, column)-pairs to the value of the elements.
- List of Lists: stores one list per row, with each entry containing the column index and the value.
- Coordinate List: a list of (row, column, value) tuples.
- Compressed Sparse Row: three (one-dimensional) arrays (A, IA, JA).
- Compressed Sparse Column: same as SCR
- example
- covert to sparse matrix
python: csr_matrix(dense_matrix) - covert to dense matrix
python: sparse_matrix.todense() - sparsity = 1.0 – count_nonzero(A) / A.size
- covert to sparse matrix
- sparsity score =
- Tensor
- multidimensional array.
- algriothm is similar to matrix
- dot product:
python: tensordot()
- upper letter.
Factorization
- Matrix Decompositions
- LU Decomposition
- square matrix
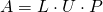 , L is lower triangle matrix, U is upper triangle matrix. P matrix is used to permute the result or return result to the orignal order.
, L is lower triangle matrix, U is upper triangle matrix. P matrix is used to permute the result or return result to the orignal order.python: lu(square_matrix)
- QR Decomposition
- n*m matrix
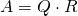 where Q a matrix with the size mm, and R is an upper triangle matrix with the size mn.
where Q a matrix with the size mm, and R is an upper triangle matrix with the size mn.python: qr(matrix)
- Cholesky Decomposition
- square symmtric matrix where values are greater than zero
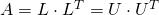 , L is lower triangle matrix, U is upper triangle matrix.
, L is lower triangle matrix, U is upper triangle matrix.- twice faster than LU decomposition.
python: cholesky(matrix)
- EigenDecomposition
- eigenvector:
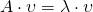 ,
, 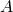 is matrix we want to decomposite,
is matrix we want to decomposite, 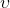 is eigenvector,
is eigenvector, 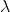 is eigenvalue(scalar)
is eigenvalue(scalar) - a matrix could have one eigenvector and eigenvalue for each dimension. So the matrix
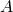 can be shown as prodcut of eigenvalues and eigenvectors.
can be shown as prodcut of eigenvalues and eigenvectors. 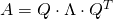 where Q is the matrix of eigenvectors,
where Q is the matrix of eigenvectors, 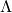 is the matrix of eigenvalue. This equotion also mean if we know eigenvalues and eigenvectors we can construct the orignal matrix.
is the matrix of eigenvalue. This equotion also mean if we know eigenvalues and eigenvectors we can construct the orignal matrix. python: eig(matrix)
- eigenvector:
- SVD(singluar value decomposition)
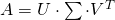 , where A is m*n, U is m*m matrix,
, where A is m*n, U is m*m matrix, 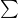 is m*m diagonal matrix also known as singluar value,
is m*m diagonal matrix also known as singluar value, 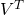 is n*n matrix.
is n*n matrix.python: svd(matrix)- reduce dimension
- select top largest singluar values in
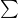
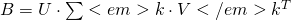 , where column select from
, where column select from 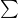 , row selected from
, row selected from 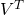 , B is approximate of the orignal matrix A.
, B is approximate of the orignal matrix A.- `python: TruncatedSVD(n_components=2)
- select top largest singluar values in
- LU Decomposition
Stats
- Multivari stats
- variance:
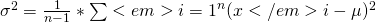 ,
, python: var(vector, ddof=1) - standard deviation:
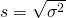 ,
, python:std(M, ddof=1, axis=0) - covariance:
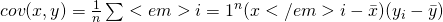 ,
, python: cov(x,y)[0,1] - coralation:
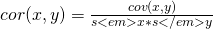 , normorlized to the value between -1 to 1.
, normorlized to the value between -1 to 1. python: corrcoef(x,y)[0,1] - PCA
- project high dimensions to subdimesnion
- steps:
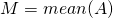
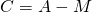
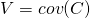
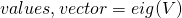
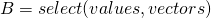 , which order by eigenvalue
, which order by eigenvalue
- scikit learn
pca = PCA(2) # get two components
pca.fit(A)
print(pca.componnets_) # values
print(pca.explained_variance_) # vectors
B = pca.transform(A) # transform to new matrix
- Linear Regression
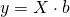 , where b is coeffcient and unkown
, where b is coeffcient and unkown- linear least squares( similar to MSE)
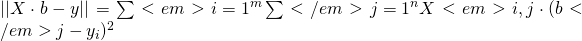 , then
, then  . Issue: very slow
. Issue: very slow - MSE with SDG
- variance:
Reference: Basics of Linear Algebra for Machine Learning, jason brownlee, https://machinelearningmastery.com/linear_algebra_for_machine_learning/
Leave a Reply