This is a unbelievable discovery from PETER B. DENTON, STEPHEN J. PARKE, TERENCE TAO, AND XINING ZHANG. The original paper you can find here. In a short nut, we can get eiganvector through eiganvalues only. This magic formular is like blew:
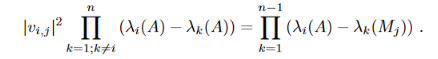
Currently, I don’t know or image what will effect on the road, but the eiganX is the basic for AI, dimension reduction, feature extraction, etc. It also may help us improve the speed to get eiganvector if we need to incrementally add data on a known matrix.
I wrote a very simple python script to prove this formula(surely, it is correct). I think it can archive by GPU as well.
import numpy as np
from numpy import linalg as LA
matrix_size = 6
org_x = np.diag(range(1,matrix_size+1))
w, v = LA.eig(org_x)
print("orgnal matriax: \n %s \n" % org_x)
print("eigan values: \n %s \n" % w)
print("normalized eigenvectors: \n %s \n" % v)
print("START NEW ALGORITHM \n")
result=[]
for _ in range(matrix_size):
result.append(0)
for n in range(matrix_size):
for j in range(matrix_size):
sub_x = np.delete(org_x,j,axis=0)
sub_x = np.delete(sub_x,j,axis=1)
w1,v1 = LA.eig(sub_x)
# in term of new formula to get orignal matrix eigenvecotr through eiganvalue
numberator = 1
denominator = 1
for i in range(matrix_size-1):
temp_n = w[n] - w1[i]
numberator = numberator*temp_n
for i in range(matrix_size):
if(i!=n):
temp_d = w[n] - w[i]
denominator = denominator*temp_d
result[j] = numberator/denominator
print("%s \n" % result)result:
orgnal matriax:
[[1 0 0 0 0 0]
[0 2 0 0 0 0]
[0 0 3 0 0 0]
[0 0 0 4 0 0]
[0 0 0 0 5 0]
[0 0 0 0 0 6]]
eigan values:
[1. 2. 3. 4. 5. 6.]
normalized eigenvectors:
[[1. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0.]
[0. 0. 1. 0. 0. 0.]
[0. 0. 0. 1. 0. 0.]
[0. 0. 0. 0. 1. 0.]
[0. 0. 0. 0. 0. 1.]]
START NEW ALGORITHM
[1.0, -0.0, -0.0, -0.0, -0.0, -0.0]
[0.0, 1.0, -0.0, -0.0, -0.0, -0.0]
[0.0, 0.0, 1.0, -0.0, -0.0, -0.0]
[0.0, 0.0, 0.0, 1.0, -0.0, -0.0]
[0.0, 0.0, 0.0, 0.0, 1.0, -0.0]
[0.0, 0.0, 0.0, 0.0, 0.0, 1.0]Reference:
EIGENVECTORS FROM EIGENVALUES, https://arxiv.org/pdf/1908.03795.pdf
Tao’s Blog, https://terrytao.wordpress.com/2019/08/13/eigenvectors-from-eigenvalues/
Leave a Reply